LEIBNIZ ÉS A MONÁSZOK

(Reuben Hersh: A matematika természete c. könyv 133. oldaláról)
Gyönyörûen írja le Leibniz világát
Gottfried Martin (1.o.-tól folytatólagosan)
" Minden monászt elõször élõként
ír le. Egy merész ugrással tehát az egész
Univerzum élõlények, azaz monászok sûrû
tengere. Minden él; az Univerzumban mindaz, ami terméketlen,
steril, halott, csupán illúzió. ... Az élõ
dolgoknak eme hatalmas óceánjában nincsenek üres
helyek. Ahová csak tekintünk, teremtmények, élõlények,
állatok, entelecheiák és lelkek nyüzsögnek.
Minden parányi anyagrészecske, legyen az bármilyen
apró, növényekkel teli kert, halaktól hemzsegõ
tavacska, és e kert minden növényének minden
apró ágacskája, és e tavacska halainak minden
parányi vércseppje újabb növényekkel
teli kert, halakban dúskáló tavacska és így
tovább, a végtelenségig. A végtelenül
nagyban és a végtelenül parányiban mindenütt
van élet, mindenütt vannak monászok. Minden egyes monász
érzékel, és akarata van. ... (Saját megjegyzésem:
A végtelenül parányi monászok Leibniz matematikai
infinitezimálisaira emlékeztetnek - Leibniz matematikája
és metafizikája összecseng.)"
Martin így folytatja: "A monászok egyedi létén
kívül és azok között nem-valóság
van. Miután ebben az értelemben csak a monászok és
módosulataik rendelkeznek valóságos léttel,
a relációk léte nem lehet valóságos
... vagy másképpen, Leibniz gyakori kifejezésével,
csak mentális értelemben léteznek ... A relációk
közé tartoznak a számok, az idõ, idõtartam,
a tér, a testek kiterjedése ... Ám a relációkat
elgondoló értelem Isten értelme. Azáltal,
hogy a relációkat egy értelem alá utalja,
megfosztja õket szubsztanciális valóságuktól,
ám minthogy isteni értelem hordozza õket ... ismét
visszanyernek egy újfajta létezést ..." Na,
eddig Martin.
Leibniz metafizikája magával ragadó fantáziavilág.
Monadológiáját Savoyai Jenõ herceg
kérésére írta meg (Carr, 3.o) Idealisztikus
atomizmusa vezeti arra a gondolatra, hogy létezniük kell olyan
"egyszerû" részeknek vagy "monászoknak",
amelyekbõl az egész világ áll. Tehát
mindaz, ami valóságos, nem létezhet a monászokon
kívül. Ebbõl következõen például
a monászok közötti relációk sem lehetnek
valóságosak. Nem láthatják egymást,
"ablaktalanok". Na, eddig Reuben Hersh.
Véleményem szerint Leibniz magukat a kvadronokat pillantotta
meg. Egy lényeges különbség az, hogy Leibniz a
monászait ablaktalanoknak képzelte el, márpedig a
kvadronok legszembetûnõbb vonása az, hogy tükrözik
egymást és önmagukat. Ebbõl az önegymástükrözésbõl
szövõdik aztán az, amit isteni értelemnek nevezhetünk,
és amely mindent magába foglal. Ennek gyönyörû
modellje a Mandelzum. A Mandelzum abban különbözik a Mandelbrot-halmaztól,
hogy az aurát is magába foglalja. Épp az aurából
erednek a gyönyörû színek! Leibniz szerint a dolgok
paralellitása csak látszólagos, egy isteni Harmónia
Prestabilita miatt mutatja két óra ugyanazt a pontos idõt,
és ha két ember beszélget, valójában
mindkettõ monológot mond, csak az isteni elmében
fognak ezek összecsengeni. Szerintem viszont az önegymástükrözés
valóságos, és így a kvadronok kapcsolatai,
relációi is valóságosak. De az is igaz, hogy
ezek egy isteni elmében tükrözõdõ fogalmak!
Tehát a fogalmak valóságosak, tehát a szellemvilág:
Valóság!
Sõt, a szellemvilág valósága magasabbrendû,
objektívabb, mert a 2•2 akkor is 4 lesz, amikor az utolsó
csillag is kilobbant az égen. A Szellemvilág Valóságának
formái áramlanak be a kritikus pontokon át a mi világunkba.
Ezek az elsõdleges teremtõ erõk, melyek a világot
és az embert kiformálják.
Én így írom le ugyanezt: Minden táncol, minden
él, minden lüktet, és részt vesz az egyetemes
Táncban, amit istenek koreografáltak, minden pici kis részecske
tudatos, és tudja, hol a helye, tánca nem önkényes
szeszély, hanem hatalmas titkok hordozója, egyetlen pici
amõba mozgásából kikódolható
a Mindenség összes titka. Aki odafigyel - és a nagy
tudósok : Pasteur, Koch, Röntgen, Madame Curie, Fleming odafigyeltek
- az meglátja a Titkok Titkát, egy-egy újabb fejezetét
a Tudomány fejlõdésének! Mi magunk is e Tánc
részei vagyunk, akkor is amikor a legreménytelenebb az életünk,
amikor a legmagányosabbak vagyunk, Valaki figyel és számontart
minket, végszavaink elhangzanak, és a láthatatlan
erõk mozgásba lendülnek. Sosem vagyunk egyedül.
Sosem vagyunk elveszettek. A Show folytatódik akkor is, amikor
látszólag abbamarad. A stafétát mindig továbbadjuk,
akkor is ha nem tudunk róla. Talán egy elejtett megjegyzésünk,
egy eldobott papírfecnink, amit valaki fölvesz, egy mozdulatunk
... mindez mag, mely új élet hordozója. Bennünk
ragyog a Mindenség Prímfénye. Ez az életérzés
az Uranita hit szíve.
Én és a Mindenség egyek vagyunk. Sebei rajtam nyílnak
fel, örömei bennem oldódnak fénnyé. Felelõs
vagyok mindenért. Ha esik az esõ, miattam esik, ha süt
a nap, értem süt.
Ha szenved a világ, miattam szenved. Segítsünk hát
rajta, minden erõnkkel, szenteljük neki az életünket,
akkor nem lesz egyetlen hiábavaló percünk se. Amit
Leibniz leír, az maga a Nagy Fraktál, a Mindenség
Mandelzuma, és Leibniz látta a Mandelbrot halmazt, valami
rejtélyes beavatás megmutatta neki, ahogy a tibetiek is
látták, és én is láttam, még
az elsõ megjelent Mandelbrot-képek elõtt! Nekem a
Benzin mutatta meg...
A 76-os Kvadronmodell egyik legfõbb alapeszméje a kváziazonosság
felismerése volt.
A kvadronteret bináris sorozatokból építettem
fel, mert még az apám mondta egyszer hogy pusztán
nullákból és egyesekbõl leírható
az egész Mindenség! Ez az eszme rendkívül megragadott
engem. Aztán a BME-n dr. Prékopa Andrástól
tanultunk analízist, és ott döbbenetes titkok derültek
ki. Pl. az, hogy a síknak ugyanannyi pontja van mint az egyenesnek.
Na hiszen, akkor léteznie kell egy-egy értelmû leképezésnek
is az egyenesrõl a síkra és viszont! Papy Topológia
könyvébõl aztán megtudtam, hogy ez így
is van, Peano-görbének nevezik az illetõ jószágot,
és ez bizony fraktál a javából! Mindez 73-74-75-ben,
amikor nálunk még híre sem volt Mandelbrotnak! Ismertem
a Sierpinski-szõnyeget és a Cantor-halmazt is, ennyi nekem
elég is volt ahhoz hogy egy merõben új világ
bontakozzon ki a szemem elõtt! No nem a fraktálok! Mert
amit én megláttam, az messze több a fraktáloknál!
Elképzeltem hogy az elektronok olyanok mint a bolygók, egész
világok, melyeken icipici kis emberkék élnek, akiknek
az idejük arányosan gyorsabb, tehát egyetlen másodperc
alatt évmilliárdokat élnek át. Ehhez hasonlóan,
a galaxisok nem egyebek mint egy gigászi világ atomjai,
ahol viszont az idõ irdatlanul lassan telik, évmilliárdok
alatt telik el náluk egy másodperc! Számomra mindig
is élõ ige volt Hermész Triszmegisztosz mondása:
Amilyen a Nagyvilág, szakasztott olyan a Kisvilág! Ez felfogható
egyfajta fraktáltörvénynek is! Aztán tanultunk
Mértékelméletet is, ami újabb misztériumok
forrása volt! Például a szigma-additivitás.
Kiderült, hogy a végtelen összegekkel baj van. 0+0+0+0
... =0, ám ha a>0, akkor a akármilyen pici is, a+a+a+a
…= végtelen lesz. Nem tudunk végtelen darab egyforma
számot úgy összeadni, hogy az eredmény véges
maradjon. Node hiszen Leibniz erre találta ki az epszilont! Vagyis
az infinitezimálist! Legyen  így definiálva:
így definiálva:  +
+ +
+ +
+ ... =1! Mekkora vajon
... =1! Mekkora vajon  ?
Nyilván kisebb bármely pozitív valós számnál!
Tehát ez a régóta keresett infinitezimális!
Jelöljük a végtelent így:
?
Nyilván kisebb bármely pozitív valós számnál!
Tehát ez a régóta keresett infinitezimális!
Jelöljük a végtelent így: 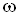 .
Ekkor
.
Ekkor  +
+ +
+ +
+ ... =
... =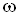 •
• =1
lesz. Mekkora
=1
lesz. Mekkora  négyzete?
Most erre két választásunk van. Vagy azt mondjuk
hogy egy másodrendû infinitezimális, ami még
négyzete?
Most erre két választásunk van. Vagy azt mondjuk
hogy egy másodrendû infinitezimális, ami még
 -nál is sokkal picibb,
vagy egyszerûen azt modjuk hogy nulla! Tehát
-nál is sokkal picibb,
vagy egyszerûen azt modjuk hogy nulla! Tehát  •
• =0
! Ekkor a valós számokból és az
=0
! Ekkor a valós számokból és az  -ból
egy ún. parabolikus komplex számot csinálhatunk:
a+b•
-ból
egy ún. parabolikus komplex számot csinálhatunk:
a+b• . Két ilyen
számot meg egyszerûen úgy szorzunk, hogy minden tagot
minden taggal, és figyelembevesszük, hogy
. Két ilyen
számot meg egyszerûen úgy szorzunk, hogy minden tagot
minden taggal, és figyelembevesszük, hogy  •
• =0!
Tehát (a+b•
=0!
Tehát (a+b• )×(
c+d•
)×(
c+d• )=a•c+a•d•
)=a•c+a•d• +b•c•
+b•c• +b•d•
+b•d• •
• =a•c+a•d•
=a•c+a•d• +b•c•
+b•c• =
a•c+(a•d+b•c)•
=
a•c+(a•d+b•c)• ,
mert az utolsó tag nulla. Érdekes mód ennek a világnak
van modellje, mégpedig a 2•2-es mátrixok körében:
a+b•
,
mert az utolsó tag nulla. Érdekes mód ennek a világnak
van modellje, mégpedig a 2•2-es mátrixok körében:
a+b• = |a b| Ezeket
a mátrixokat a szokásos módon szorozva egymással,
épp a kívánt viselkedést |0 a| kapjuk. Ebben
a világban a deriválást nagyon könnyû
elvégezni. A differenciálhányados egyszerûen
= |a b| Ezeket
a mátrixokat a szokásos módon szorozva egymással,
épp a kívánt viselkedést |0 a| kapjuk. Ebben
a világban a deriválást nagyon könnyû
elvégezni. A differenciálhányados egyszerûen
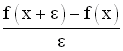 , pl.
, pl.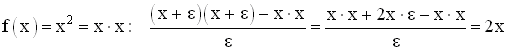 .
.
Minden különösebb határértékkel való
vacakolás nélkül megkaptuk a helyes eredményt.
(Én viszont nagyon sokat vacakoltam, mire ezt bepötyögtem
a gépbe!)
Sokkal érdekesebb az a verzió, ahol  •
• nem nulla! Hanem egy másodrendû infinitezimális, mondjuk
nem nulla! Hanem egy másodrendû infinitezimális, mondjuk
 2! És
így
2! És
így  •
• •
• =
= 3,
3,
 •
• •
• •
• =
= 4,
stb... Az
4,
stb... Az  reciptroka az
reciptroka az
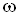 , ezt is szorozgathatom önmagával,
kapom az
, ezt is szorozgathatom önmagával,
kapom az 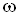 2,
2, 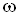 3,
3,
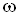 4-eket, amik a makrovilágot
testesítik meg.
4-eket, amik a makrovilágot
testesítik meg.
Ez a fejtegetés viszont azt a látszatot kelti, mintha mi
magunk teremtenénk ezeket a világokat, azzal hogy választunk!
Most akkor ezek objektíve léteznek, tõlünk függetlenül,
vagy mi hozzuk létre õket? Még élesebben felvetve
a problémát, vajon a számok léteztek már
a dinoszauruszok idején is? Két dinoszaurusz meg két
dinoszaurusz az ugyebár négy dinoszaurusz? Reuben Hersh
legfõbb problémája szintén ez, az egész
könyv errõl szól. Az én válaszom az,
hogy ez is, az is! Tehát a matematikai objektumok egyrészt
objektíve léteznek a szellemvilágban, másrészt
az ember amikor a szellemvilágból lehívja ezt az
információt, akkor megteremti - az anyagi világban!
Tehát a tudás, mint az emberiség közkincse,
nem mindig van jelen, mindig van valaki, aki a tudást lehozza a
Földre, lehívja az Égi Internetrõl, vagy másképpen:
kihozza a hönirt a Zónából! Ez nem mindig veszélytelen
ám! Könnyen lehet hogy a Sztalker otthagyja a fogát!
Sose tudhatja, hogy a holmi, amit éppen visz, csak úgy van,
vagy szép csendben megöli! Szóval a kvaterniók
léteztek már azelõtt is, hogy Hamilton agyából
kipattantak, csak nem képezték az emberiség tudáskincsének
részét. Mert ugyebár Kidd kapitány kincse
is létezik valahol a Kincses Szigeten elásva, csak még
nem ásta ki senki! Tut Ankh Amon sírkamrája is 3000
évig várt, mire felfedezték. De addig is megvolt.
A mûvelt matematika, mint az emberiség tudásának
része, társadalmi jelenség, a társadalomtól
nem elválasztható. De amirõl a matek szól,
az az örökkévaló dolgok világa, amely elõbb
volt mint a Világegyetem, és utána is fennmarad!
A kis zöld emberkék az NGC Galaxisból ugyanúgy
felfedezhetik a kvaterniókat, vagy akár a véges egyszerû
csoportokat is. Erdõs Pál úgy becézte Istent,
hogy a Legfelsõbb Fasiszta (LF), és a derék Teremtõ
azzal szolgált rá e névre, hogy van neki egy könyve:
A KÖNYV, amely tartalmazza az elmúlt és eljövendõ
korok összes matematikai eredményét, méghozzá
a legtisztább interpretációban, és a dög
nem engedi hogy az ilyen szegény Erdõs Palikák csak
úgy kandin belepillantsanak! Talán majd halálunk
óráján, de akkor már mi a fenét érünk
vele? Úgy tûnik, Ramanujan látta a Könyvet, és
egész fejezeteket olvasott belõle. Csak törhetjük
a fejünket, honnan szedte az eredményeit. Õ maga azt
állítja, hogy egy Namagiri nevû istennõ tanította
meg rá. Én hiszek neki, már csak azért is,
mert jómagam is eme istennõ kegyeit keresem!
Amit Namagiri istennõ tud, az készen vár már
ránk az Idõben, csak el kell utazni odáig!
A matematika nemcsak az emberiség tudásának részeként
van jelen a világban. Benne van minden fizikai, kémiai,
biológiai, társadalmi, stb. jelenségben, akkor is
ha ezt senki nem veszi észre. Egyszerûen a világ rendjének
ez az anyanyelve. Úgyhogy feltehetjük a kérdést:
Végül is mi a matematika? Szimbólumokkal végzett
játék? Számolás? Vagy emlékezés
a szellemvilágban megtapasztalt örök dolgokra? Ez is,
az is. A Mindenség Tükre és Szerelme. Nem más,
mint a Nagy Egyesülés eszköze. Prímkristály-sugárvilág.
Vagy egyszerûen csak egy gyermeki mosoly Isten arcán.
